↜ Back to index Introduction to Numerical Analysis 1
Part b—Lecture 3
Today we discuss stability of the finite difference method and another important boundary conditions for the heat equation.
Periodic boundary condition
Sometimes it is convenient not to have to worry about value of the solution on the boundary by assuming that the solution is 1-periodic function in the x-variable and satisfies the heat equation for all x \in {\mathbb{R}}. In the numerical method, we can express this by treating the values at x_0 and x_M as the same values, and the values at x_{-1} and x_{M-1} as the same values, etc.
Therefore we have only unknowns u_{n,k} for k = 0, \ldots, M-1, n \geq 0. The numerical scheme is \left\{ \begin{aligned} u_{n+1, 0} &= u_{n, 0} + \frac\tau{h^2} (u_{n, M - 1} - 2 u_{n, 0} + u_{n, 1}),\\ u_{n+1, k} &= u_{n, k} + \frac\tau{h^2} (u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}), && k = 1, \ldots, M-2,\\ u_{n+1, M-1} &= u_{n, M-1} + \frac\tau{h^2} (u_{n, M - 2} - 2 u_{n, M-1} + u_{n, 0}). \end{aligned} \right.
Notice how the indices wrap around.
Here is an example implementation in Fortran.
! Solve the heat equation with periodic boundary condition
implicit none
integer, parameter :: M = 10
real, parameter :: pi = 4. * atan(1.)
integer n, k, nmax
real h, tau, x
! 👇 We need only values up to M-1
real, dimension(0:M-1) :: u, v
h = 1. / M
tau = h * h / 4.
nmax = 0.5 / tau
do k=0, M-1
x = k * h
u(k) = sin(pi * x)
print *, 0., x, u(k)
end do
print *
do n=0, nmax-1
do k = 0, M-1
v(k) = u(k) + (tau / (h * h)) * (u(mod(k + M - 1, M)) &
- 2 * u(k) + u(mod(k + 1, M)))
end do
! print the values of the solution at t_{n+1}
do k = 0, M-1
print *, (n + 1) * tau, k * h, v(k)
end do
! print an empty line (needed for gnuplot)
print *
! store the values of v in u
u = v
end do
endTo implement the wrapping around of indices we used function mod(a, b). This function returns the remainder (余り) of division a / b. We have
\operatorname{mod}(k + M - 1, M) =
\begin{cases}
M-1, & k = 0,\\
k-1, & k = 1, \ldots, M-1,
\end{cases}
and
\operatorname{mod}(k + 1, M) =
\begin{cases}
k+1, & k = 0, \ldots, M-2,\\
0, & k = M-1.
\end{cases}
Neumann boundary condition
Now instead of prescribing the value of u at x = 0 and x = 1, we prescribe the value of the derivative u_x = \frac{\partial u}{\partial x}:
\left\{ \begin{aligned} u_t(x, t) &= u_{xx}(x, t), && 0 < x < 1, t > 0,\\ u(x, 0) &= u_0(x), && 0 < x < 1, \\ u_x(0, t) &= a, && 0 < t, \\ u_x(1, t) &= b, && 0 < t. \end{aligned} \right.
This type of boundary condition is called the Neumann boundary condition. We prescribe the value of the derivatives u_x(0, t) = \frac{\partial u}{\partial x}(0, t) and u_x(1, t) = \frac{\partial u}{\partial x}(1, t) on the boundary of the domain, instead of the value of the solution as in the case of the Dirichlet boundary condition.
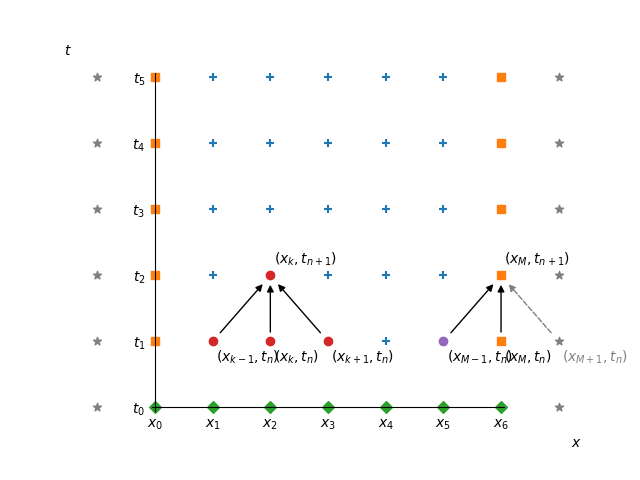
We have to modify the numerical method at the boundary since now the values u_{n, 0} and u_{n, M} are unknown. We use the difference scheme as before:
u_{n+1, k} = u_{n, k} + \frac\tau{h^2} (u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}).
However, when k = 0, we need something in place of u_{n, -1} since u_{n, -1} is a value outside of the domain. We use the second order symmetric finite difference to approximate the first derivative u_x:
u_x(x, t) = \frac{u(x + h, t) - u(x - h, t)}{2 h} + O(h^2).
Therefore we can use the value of the derivative u_x on the boundary (at x = 0 or x = 1) to estimate the value of the solution outside of the domain. Based on the above formula at x = 0, we use u_{n, -1} = u_{n, 1} - 2 h a. Similarly, at x = 1 we use u_{n, M + 1} = u_{n, M-1} + 2 h b. After substituting this into the scheme, we get for k = 0 and k = M the modified scheme
\begin{aligned} u_{n+1, 0} &= u_{n, 0} + \frac{2\tau}{h^2} ( u_{n, 1} - u_{n, 0} - h a),\\ u_{n+1, M} &= u_{n, M} + \frac{2\tau}{h^2} (u_{n, M-1} - u_{n, M } + h b). \end{aligned}
See the following figure for an illustration.
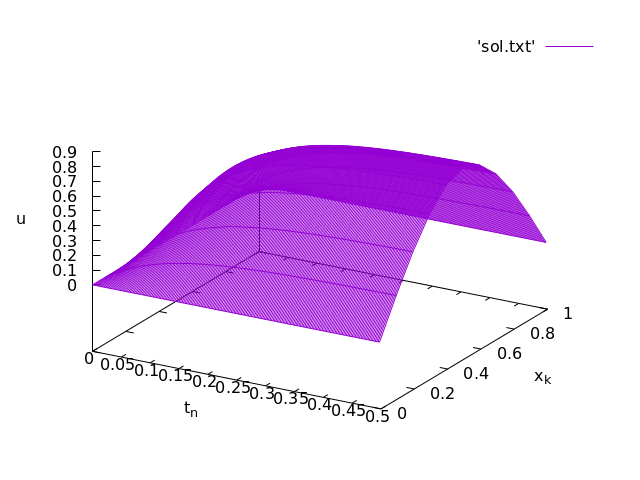
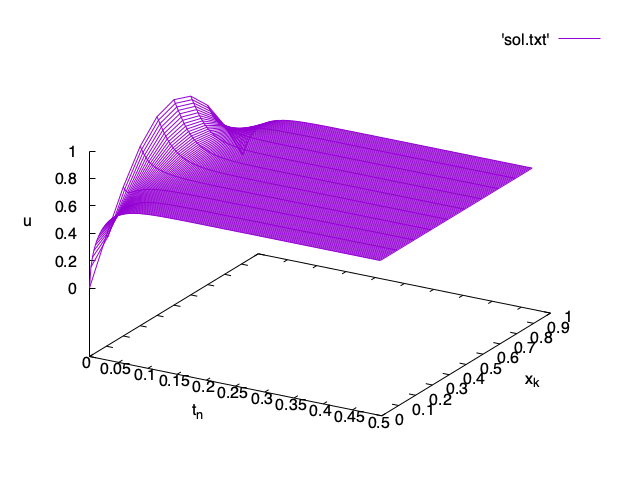
Example 1. The heat equation with initial data u_0(x) = x (1 - x) and Neumann boundary data a = 1, b = -1 has the exact solution u(x,t) = x (1 - x) - 2t.
Stability of the explicit finite difference scheme
As in the Euler method for ordinary differential equations, the time step \tau cannot be taken arbitrarily large in the finite difference scheme for the heat equation.
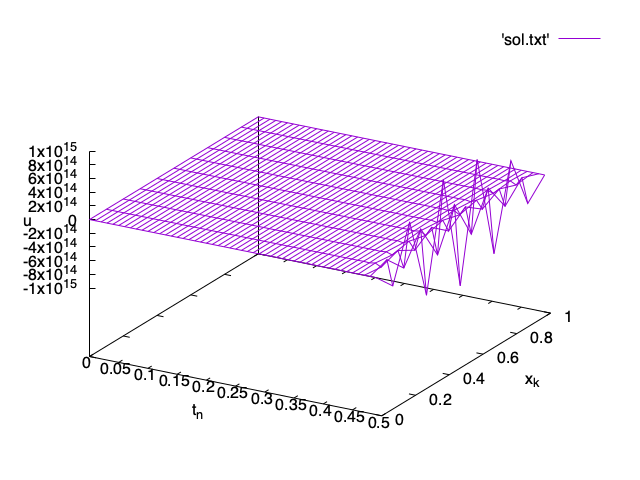
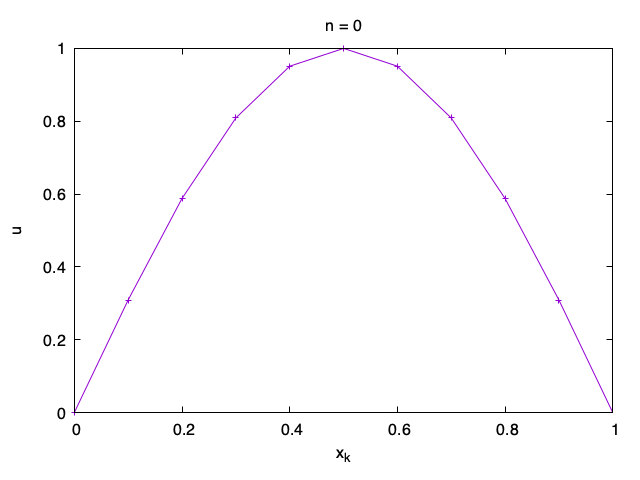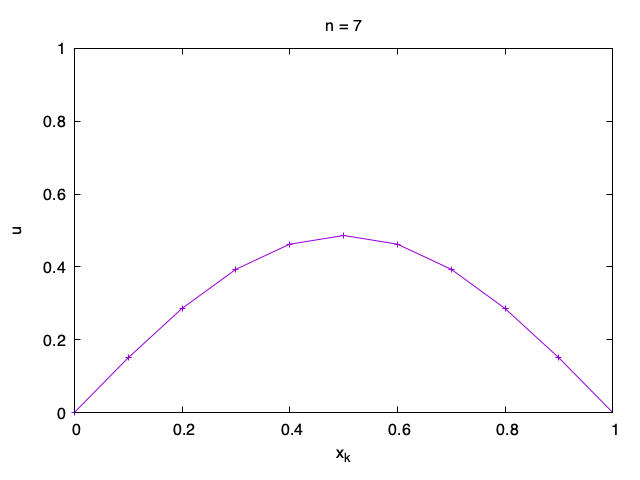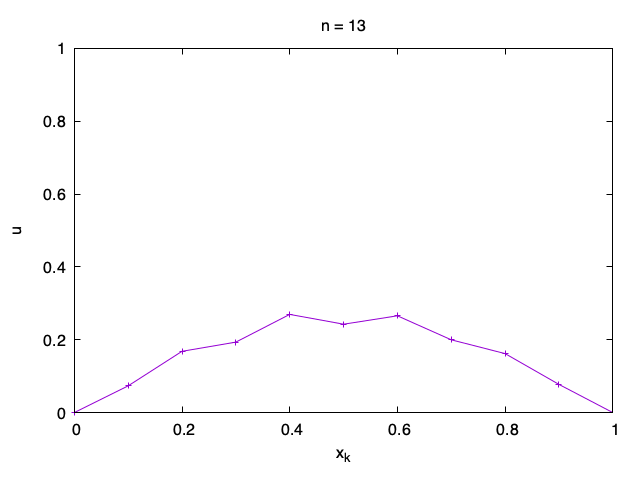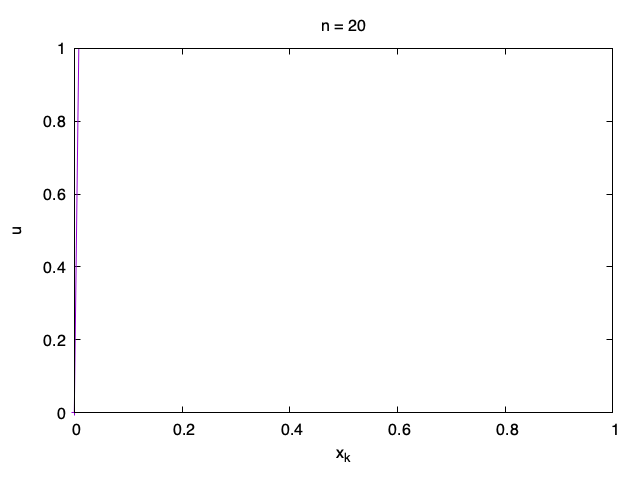
Stability condition
Here we try to investigate why this happens. Let us assume that the numerical solution at step n = 0 is u_{0, k} = \sin\left(\frac{\ell k\pi}M\right) for some \ell \in {\mathbb{N}} not divisible by M. We have u_{0, 0} = u_{0, M} = 0.
Let us see what happens if we apply the numerical method to it. Let us take the boundary values 0 and so we always set u_{n, 0} = u_{n, M} = 0. Otherwise,
u_{n+1, k} = u_{n, k} + \frac\tau{h^2} (u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}), \qquad k = 1, \ldots, M-1. To simplify the formula, let us set r := \frac\tau{h^2}. Now we can write the formula as u_{n+1, k} = r u_{n, k - 1} + (1 - 2r) u_{n, k} + r u_{n, k + 1}. Let us find u_{1, k} using the formula for u_{0, k}. We recall that \sin\left(\frac{\ell (k \pm 1)\pi}M\right) = \sin\left(\frac{\ell k\pi}M\right) \cos \left(\frac{\ell \pi}M\right) \pm \cos\left(\frac{\ell k\pi}M\right) \sin \left(\frac{\ell \pi}M\right). We therefore get u_{1, k} = \left(1 - 2r + 2r \cos \left(\frac{\ell \pi}M\right)\right)\sin\left(\frac{\ell k\pi}M\right) =\left(1 - 2r + 2r \cos \left(\frac{\ell \pi}M\right)\right) u_{0, k}. Iteratively, u_{n, k} =\left(1 - 2r + 2r \cos \left(\frac{\ell \pi}M\right)\right)^n u_{0, k}, \qquad n \geq 0. The formula for solution is quite simple. But we really do not want the term \left(1 - 2r + 2r \cos \left(\frac{\ell \pi}M\right)\right)^n to grow in size as n increases because in that case the numerical solution will blow up. Therefore we have the natural condition \left|1 - 2r + 2r \cos \left(\frac{\ell \pi}M\right)\right| \leq 1 for any \ell \in {\mathbb{N}} not divisible by M, which is equivalent to - 1 \leq 1 - 2r + 2r \cos \left(\frac{\ell \pi}M\right) \leq 1
The second inequality is always satisfied.
It is not difficult to see that that the middle term has minimum for \ell = M - 1. Since the value of \cos \left(\frac{(M-1)\pi}M\right) \approx -1, we get a condition on r for the numerical method to never blow up for any M and any possible initial data: r \leq \frac 12.
Recalling that r = \tau/h^2, we get:
Stability condition. \tau \leq \frac{h^2}2
Note that the value \frac{h^2}2 is really the limit. It is safer to take a smaller value like \frac{h^2}4 to avoid any possible issues.
For more details, see von Neumann stability analysis.
This means that if we want to have a good space resolution of our method (small h), the number of time steps that we need to take becomes quickly prohibitively large. In such a case we should use a better numerical method, for instance implicit methods. But this is beyond the scope of this lecture.
Report 1
Submit the report to LMS by July 12 (Monday), 17:00.
Exercise 1.
Write the Fortran code for the heat equation with periodic boundary condition. Use initial data
u_0(x) = \cos(2 \pi x)
In producing the figures, use h = 1/M and \tau = h^2 / 4.
- Submit the plot of the solution M =10 on time interval [0, 0.125] to LMS. Use your student ID number as the title. 問1
Modify the code to output the errors |u_{n, k} - u(x_k, t_n)| where the exact solution is u(x,t) = e^{-4\pi^2 t} \cos(2 \pi x).
Submit the plot of the error for M =10 on time interval [0, 0.125] to LMS. Use your student ID number as the title. 問2
Submit the plot of the error for M =20 on time interval [0, 0.125] to LMS. Use your student ID number as the title. 問3
Submit the Fortran code use for producing data for plot in 3. 問4
Exercise 2.
Write the Fortran code for the heat equation with Neumann boundary condition. Use the initial data and boundary data from Example 1:
u_0(x) = x (1 - x), \quad a = 1, \quad b = -1
In producing the figures, use h = 1/M and \tau = h^2 / 4.
- Submit the plot of the solution with M =10 on time interval [0, 0.5] to LMS. Use your student ID number as the title. 問5
Modify the code to output the errors |u_{n, k} - u(x_k, t_n)| where the exact solution is u(x,t) = x(1 - x) - 2t.
Submit the plot of the error for M =10 on time interval [0, 0.5] to LMS. Use your student ID number as the title. 問6
Submit the plot of the error for M =20 on time interval [0, 0.5] to LMS. Use your student ID number as the title. 問7
Submit the Fortran code use for producing data for plot in 3. 問8
Exercise 3.
In this exercise consider the heat equation with a given f and Dirichlet boundary condition.
u_t = u_{xx} + f
Here f = f(x,t) is a given function.
In this case the finite difference scheme is
\left\{ \begin{aligned} u_{n+1, 0} &= a,\\ u_{n+1, k} &= u_{n, k} + \frac\tau{h^2} (u_{n, k - 1} - 2 u_{n, k} + u_{n, k + 1}) + \tau f(x_k, t_n), \qquad k = 1, \ldots, M - 1,\\ u_{n+1, M} &= b. \end{aligned} \right.
Solve the heat equation with the source f = 10 - 20|x - \tfrac 12|, initial data u_0(x) = 0, boundary data a = b = 0 for the Dirichlet condition.
Submit the plot of the solution with M =10 on time interval [0, 0.5] to LMS. Use your student ID number as the title. 問9
Submit the Fortran code use for producing data for plot in 1. 問10
Example solutions
1-3.
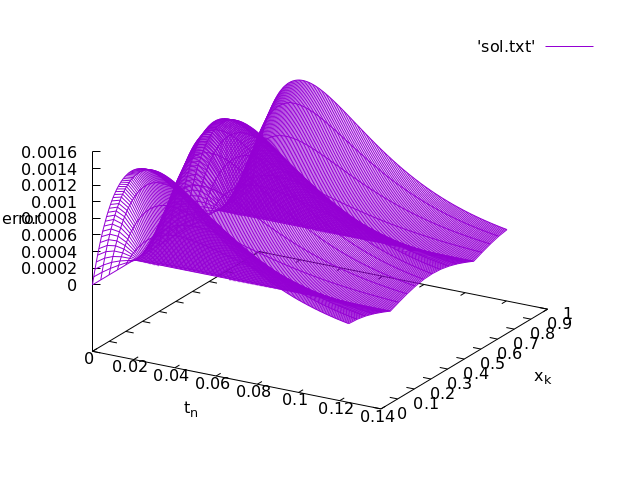
2-2.
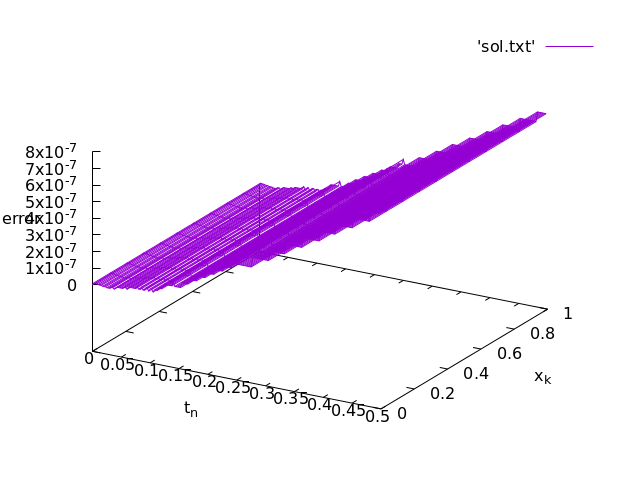
3-1.